|
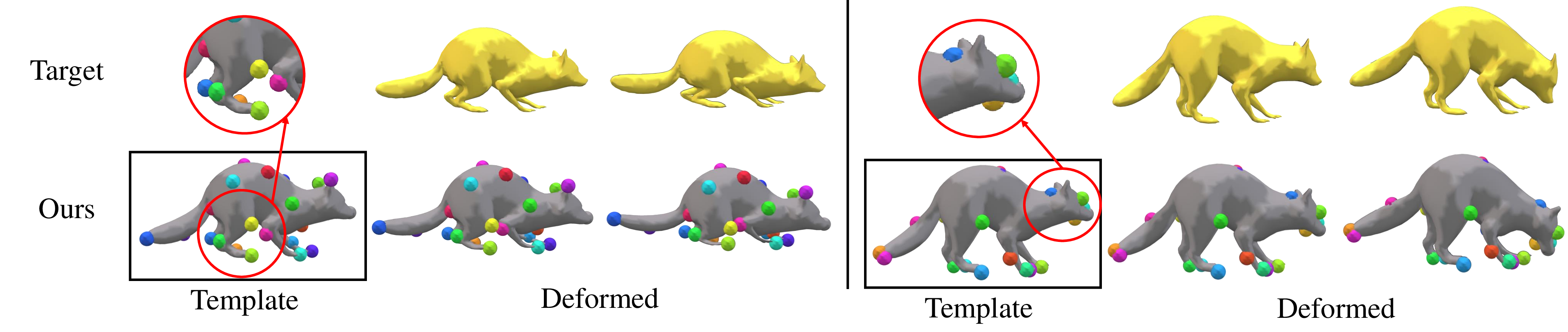
We present a data-driven framework for optimizing the sparse set of control points for biharmonic 3D shape deformation.
Control-point-based 3D deformation methods are popular techniques for interactive shape editing, whose usability can be maximized when the set of control points remains sparse while their positions are optimally distributed over the shape.
To this end, we introduce a data-driven approach capable of finding the best set of control points while assuming that the possible variations of the shape are given.
This a challenging combinatorial optimization problem since the control points need to be chosen as a subset of mesh vertices.
We address this problem by Gumbel-softmax-based continuous relaxation and a gradient-descent optimization.
We also find that the large-scale linear system involved in the biharmonic weight calculation requires heavy computation in gradients.
Thus, we reformulate this calculation to make the gradient computation 30 times faster.
Our experimental results on SMPL, SMAL, and DeformingThings4D demonstrate the effectiveness of our method compared to the farthest point sampling and a neural-network-based keypoint prediction method.
|